第5节

　　我们通常所用的数都是十进制数。这就是说，它们是按１０的幂来进位的。我们写７２９１时，实际上就是７×１０３加上２×１０２加上９×１０１加上１×１００。应当记住，

　　１０３＝１０×１０×１０＝１０００；

　　１０２＝１０×１０＝１００；

　　１０１＝１０；

　　１００＝１。

　　因此，７２９１就是７×１０００加上２×１００加上９×１０再加上１。读出声的时候，就是七千二百九十一。

　　由于我们对应用１０的各次幂已经非常习惯，所以我们只须写出他们所乘的数（如７２９１），其余的都可以略去。

　　其实，１０的幂次并不是什么神秘的东西。任何一个比一大的数的幂次都可以起到这样的效果。例如，假定我们现在想用８的幂来写出７２９１这个数，这时应当记住

　　８０＝１；

　　８１＝８；

　　８２＝８×８＝６４；

　　８３＝８×８×８＝５１２；

　　８４＝８×８×８×８＝４０９６。

　　这样，我们就可以把７２９１写为１×８４加上６×８３加上１×８２加上７×８１再加上３×８０。（请你们自己把这个数算出来，并看看所得出的答数。）如果只写出各次幂所要乘的数字，它就应当是１６１７３。因此，我们可以说１６１７３（八进制）＝７２９１（十进制）。

　　八进制的优点在于除了０以外，你只需记住七个数字。如果你想用数字８，那你可以写出８×８３，而这就等于１×８４。因此，不管任何时候，你都可以用１来代替８。所以十进制的８等于八进制的１０；十进制的８９等于八进制的１３１，依次类推。但是，用八进制时，一个数所用的总字数要比用十进制时多。由此可见，基数越小，所用的不同数字越少，但总字数则越多。

　　当你用二十进制时，７２９１这个数将成为１８×２０２加上４×２０１再加上１１×２００。在这种情形下，如果你把１８写为＃，并把１１写为％，你就可以说＃４％（二十进制）＝７２９１（十进制）。用二十进制时你将不得不用１９个不同的数字，但是每一个数所用的总字数就会少些。

　　十进制是一种很方便的进位制。用这种进位制时，既不必记住过多的数字，而且在写一个数时，又可不必用过多的字数。

　　什么是二进制数呢？在二进制的情况下，７２９１这个数等于１×２１２加上１×２１１加上１×２１０加上０×２９加上０×２８加上０×２７加上１×２６加上１×２５加上１×２４加上１×２３加上０×２２加上１×２１再加上１×２０。（请你们自己把这个数算出来，看看得出什么结果。但要记住２９是９个２的乘积，亦即２×２×２×２×２×２×２×２×２＝５１２。）如果只写出数字，那就是１１１０００１１１１０１１（二进制）＝７２９１（十进制）。

　　由于二进制数只需要用两个数字，即１和０，所以做加法和乘法演算特别简单。但是即使一个很小的数，例如７２９１，也要用很多位数表示，因而很容易在我们头脑中造成混乱。

　　但是，电子计算机则可以使用一个双向开关。把开关拨向某一方向，即把电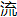接通时，它就代表１。把开关拨向另一方向，即把电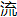断开时，它就代表０。这样，通过操纵电路，使它根据二进制的加法和乘法规则接通和断开，计算机就能以非常快的速度进行算术演算。同按十进制原理设计、用标有０到９的齿轮来进行演算的普通台式计算器相比，它的演算速度要快得多。